XGboost: A Scalable Tree Boosting System论文及源码导读
这篇论文一作为陈天齐,XGBoost是从竞赛pk中脱颖而出的算法,目前开源在github,和传统gbdt方式不同,XGBoost对loss function进行了二阶的泰勒展开,并增加了正则项,用于权衡目标函数的下降和模型的复杂度[12]。罗列下优势:
- 可扩展性强
- 为稀疏数据设计的决策树训练方法
- 理论上得到验证的加权分位数略图法
- 并行和分布式计算
- 设计高效核外计算,进行cache-aware数据块处理
分布式训练树模型boosting方法已有[1,2,3]。
整体目标
$$L\left( \phi \right) = \sum\limits_i {l\left( {{{y_i},{\hat y}_i}} \right)} + \sum\limits_k {\Omega \left( {{f_k}} \right)} $$其中$L\left( \cdot \right)$为目标函数,$l(\cdot)$是损失函数,通常是凸函数,用于 刻画预测值${{{\hat y}_i}}$和真实值${{y_i}}$的差异,第二项$\Omega \left( \cdot \right)$为模型的正则化项, 用于降低模型的复杂度,减轻过拟合问题,类似的正则化方法可以在引文[4]看到。模型目标是最小化目标函数。
$L\left( \cdot \right)$为函数空间上的表达,我们可以将其转换为下面这张gradient boosting的方式,记${\hat y}^{(t)}_i$为第$i$个样本第$t$轮迭代:
$${L^{\left( t \right)}} = \sum\limits_{i = 1}^n {l\left( {{y_i},{{\hat y}_i}^{\left( {t - 1} \right)} + {f_t}\left( {{{\bf{x}}_i}} \right)} \right)} + \Omega \left( {{f_t}} \right)$$
对该函数在${\hat y}^{(t)}_i$位置进行二阶泰勒展开,可以加速优化过程,我们得到目标函数的近似:
$${L^{\left( t \right)}} \simeq \sum\limits_{i = 1}^n {\left[ {l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right) + {g_i}{f_t}\left( {{{\bf{x}}_i}} \right) + {1 \over 2}{h_i}f_t^2\left( {{{\bf{x}}_i}} \right)} \right]} + \Omega \left( {{f_t}} \right)$$
泰勒展开的推导部分,可以参考思考1,其中第一项是常数项,删除可得:
$${{\tilde L}^{\left( t \right)}} = \sum\limits_{i = 1}^n {\left[ {{g_i}{f_t}\left( {{{\bf{x}}_i}} \right) + {1 \over 2}{h_i}f_t^2\left( {{{\bf{x}}_i}} \right)} \right]} + \Omega \left( {{f_t}} \right)--(1)$$
下面对正则化项进行参数化定义。延续前文GBDT的概念,引入分裂节点$j$定义的区域记作$${I_j} = \left\{ {i|q\left( {{{\bf{x}}_i}} \right) = j} \right\}$$
那么$\Omega$展开原目标函数改写为:
$$\eqalign{
& {{\tilde L}^{\left( t \right)}} = \sum\limits_{i = 1}^n {\left[ {{g_i}{f_t}\left( {{{\bf{x}}_i}} \right) + {1 \over 2}{h_i}f_t^2\left( {{{\bf{x}}_i}} \right)} \right]} + \gamma T + {1 \over 2}\lambda \sum\limits_{j = 1}^T {w_j^2} \cr
& \;\;\;\;\;{\rm{ = }}\sum\limits_{j = 1}^T {\left[ {\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right){w_j} + {1 \over 2}\left( {\sum\limits_{i \in {I_j}} {{h_i}} + \lambda } \right)w_j^2} \right]} + \gamma T \cr} --(2)$$
对于固定的树结构$q(x)$,对$w_j$求导得解析解$w^*_j$:
$$w_j^* = {{\sum\limits_{i \in {I_j}} {{g_i}} } \over {\sum\limits_{i \in {I_j}} {{h_i} + \lambda } }}$$
代入到$(1)$式中,可得
$${{\tilde L}^{\left( t \right)}}\left( q \right) = - {1 \over 2}{{{{\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right)}^2}} \over {\sum\limits_{i \in {I_j}} {{h_i} + \lambda } }} + \gamma T--(3)$$
公式$(3)$可以作为分裂节点的打分,形式上很像CART树纯度打分的计算,区别在于它是从目标函数中推导而得。图中显示目标函数值的计算: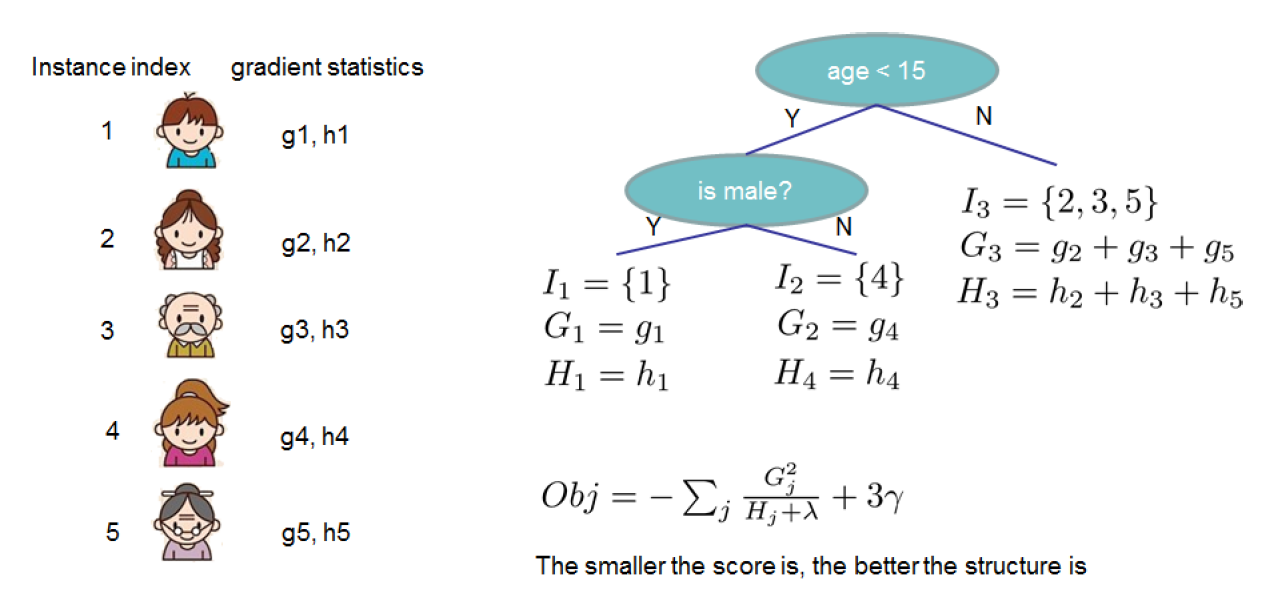
实践中,很难去穷举每一颗树进行打分,再选出最好的。通常采用贪心的方式,逐层选择最佳的分裂节点。假设$I_L$和$I_R$为分裂节点的左右节点,记$I=I_L \cup I_R$。
则选择此节点分裂的收益为:
$${L_{split}} = {1 \over 2}\left[ {{{{{\left( {\sum\limits_{i \in {I_L}} {{g_i}} } \right)}^2}} \over {\sum\limits_{i \in {I_L}} {{h_i} + \lambda } }} + {{{{\left( {\sum\limits_{i \in {I_J}} {{g_i}} } \right)}^2}} \over {\sum\limits_{i \in {I_J}} {{h_i} + \lambda } }} - {{{{\left( {\sum\limits_{i \in I} {{g_i}} } \right)}^2}} \over {\sum\limits_{i \in I} {{h_i} + \lambda } }}} \right] - \gamma \;\;-- (4)$$
[补充]
1.作为GB类方法,也可以采用shrinkage策略
2.随机森林[5]的特征降采样(subsampling)克服过拟合代码,xgboost用了类似的技术。和传统的降采样不同,xgboost按列进行降采样,在并行化有加速作用。(待研究)
查找分裂节点(split finding)
贪心算法
贪心算法是最基本的方法,前面介绍的时候有提过。具体做法:遍历所有特征中可能的分裂点位置,根据公式$(4)$找到最合适的位置。$Split\_Finding()$算法流程如下
$$\eqalign{
& Split\_Finding(): \cr
& Input:I,instance\;set\;of\;current\;node \cr
& Input:d,feature\;dimension \cr
& gain \leftarrow 0 \cr
& G \leftarrow \sum\limits_{i \in I} {{g_i}} ,H \leftarrow \sum\limits_{i \in I} {{h_i}} \cr
& for\;k = 1\;to\;m\;do \cr
& \;\;\;\;{G_L} \leftarrow 0,{H_L} \leftarrow 0 \cr
& \;\;\;\;for\;j\;in\;sorted\left( {I,by\;{{\bf{x}}_{jk}}} \right)\;do \cr
& \;\;\;\;\;\;\;\;{G_L} \leftarrow {G_L} + {g_j},{H_L} \leftarrow {H_L} + {h_j} \cr
& \;\;\;\;\;\;\;\;{G_R} \leftarrow G - {G_L},{H_R} \leftarrow H - {H_L} \cr
& \;\;\;\;\;\;\;\;score \leftarrow \max \left( {score,{{G_L^2} \over {{H_L} + \lambda }} + {{G_R^2} \over {{H_R} + \lambda }} - {{{G^2}} \over {H + \lambda }}} \right) \cr
& \;\;\;\;end \cr
& end \cr
& Output:\; split\_value\; with\; max \; score} $$
近似算法
如果数据不能一次读入内存,使用贪心算法效率较低。近似算法在过去也有应用[6, 7, 8]。具体描述为,对于某个特征${\bf x}_k$,找到该特征若干值域分界点$\{s_{k1}, s_{k2}, ... ,s_{kl}\}$。根据特征的值对样本进行分桶,对于每个桶内的样本统计值$G$、$H$进行累加(两个统计量含义同贪心算法),记为分界点$v$的统计量,$v$满足$\{{\bf x}_{kj}=s_{kv}\}$。最后在分界点集合上调用$Split\_Finding()$进行贪心查找,得到的结果为最佳分裂点的近似。具体如下:
$$\eqalign{
& for\;k = 1\;to\;m\;do \cr
& \;\;\;\;Propose\;{S_k} = \left\{ {{s_{k1}},{s_{k2}},...,{s_{kl}}} \right\}\;by\;percentile\;on\;feature\;k \cr
& \;\;\;\;Propose\;can\;be\;done\;per\;tree\left( {global} \right),or\;per\;split\left( {local} \right) \cr
& end \cr
& for\;k = 1\;to\;m\;do \cr
& \;\;\;\;{G_{kv}} \leftarrow = \sum\limits_{j \in \left\{ {j|{s_{k,v}} \ge {x_{jk}} > {s_{k,v - 1}}} \right\}} {{g_j}} \cr
& \;\;\;\;{H_{kv}} \leftarrow = \sum\limits_{j \in \left\{ {j|{s_{k,v}} \ge {x_{jk}} > {s_{k,v - 1}}} \right\}} {{h_j}} \cr
& end \cr
& call\;Split\_Finding\left( {} \right) \cr} $$
下面介绍找特征值域分界点$\{s_{k1}, s_{k2}, ... ,s_{kl}\}$的方法,加权分位数略图。为了尽可能地逼近最佳分裂点,我们需要保证采样后数据分布同原始数据尽可能一致。记${D_k} = \left\{ {\left( {{x_{1k}},{h_1}} \right),\left( {{x_{2k}},{h_2}} \right) \cdots \left( {{x_{nk}},{h_n}} \right)} \right\}$表示 每个训练样本的第$k$维特征值和对应二阶导数。接下来定义排序函数为$r_k(\cdot):R \rightarrow[0, +\infty)$
$${r_k}\left( z \right) = {1 \over {\sum\limits_{\left( {x,h} \right) \in {D_k}} h }}\sum\limits_{\left( {x,h} \right) \in {D_k},x < z} h $$
函数表示特征的值小于$z$的样本分布占比,其中二阶导数$h$可以视为权重,后面论述。在这个排序函数下,我们找到一组点$\{s_{k1}, s_{k2}, ... ,s_{kl}\}$ ,满足:
$$\left| {{r_k}\left( {{s_{k,j}}} \right) - {r_k}\left( {{s_{k,j + 1}}} \right)} \right| < \varepsilon$$
其中,${s_{k1}} = \mathop {\min }\limits_i {x_{ik}},{s_{kl}} = \mathop {\max }\limits_i {x_{ik}}$。$\varepsilon$为采样率,直观上理解,我们最后会得到$1/\varepsilon$个分界点。
讨论下为何$h_i$表示权重。从目标函数$(1)$出发,配方得到$$\sum\limits_{i = 1}^n {\left[ {{1 \over 2}{{\left( {{f_t}\left( {{x_i}} \right) - {g_i}/{h_i}} \right)}^2}} \right]} + \Omega \left( {{f_t}} \right) + constant$$
具体证明过程见原作附录。这是一个关于标签为${{g_i}/{h_i}}$和权重为$h_i$的平方误差形式。当每个权重相同的时候,退化为普通的分位数略图[9, 10]
接下来介绍另一个论文的亮点,寻找分裂点的过程中,如何克服数据稀疏。稀疏数据可能来自于missing value、大量的0值、或者特征工程例如采用one-hot表示带来的。为了解决这个问题,设定一个默认指向,当发生特征缺失的时候,将样本分类到默认分支,如下图: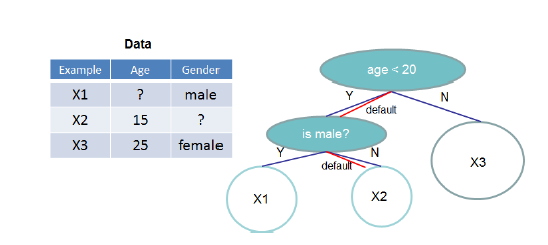
默认方向由训练集中non-missing value学习而得,把不存在的值也当成missing value进行学习和处理,如下:
$$\eqalign{
& Sparsity\_Split\_Finding(): \cr
& Input:I,instance\;set\;of\;current\;node \cr
& Input:d,feature\;dimension \cr
& gain \leftarrow 0 \cr
& G \leftarrow \sum\limits_{i \in I} {{g_i}} ,H \leftarrow \sum\limits_{i \in I} {{h_i}} \cr
& for\;k = 1\;to\;m\;do \cr
& \;\;\;\;{G_L} \leftarrow 0,{H_L} \leftarrow 0 \cr
& \;\;\;\;for\;j\;in\;sorted\left( {I_k,ascent order by\;{{\bf{x}}_{jk}}} \right)\;do \cr
& \;\;\;\;\;\;\;\;{G_L} \leftarrow {G_L} + {g_j},{H_L} \leftarrow {H_L} + {h_j} \cr
& \;\;\;\;\;\;\;\;{G_R} \leftarrow G - {G_L},{H_R} \leftarrow H - {H_L} \cr
& \;\;\;\;\;\;\;\;score \leftarrow \max \left( {score,{{G_L^2} \over {{H_L} + \lambda }} + {{G_R^2} \over {{H_R} + \lambda }} - {{{G^2}} \over {H + \lambda }}} \right) \cr
& \;\;\;\;end \cr
& \;\;\;\;{G_R} \leftarrow 0,{H_R} \leftarrow 0 \cr
& \;\;\;\;for\;j\;in\;sorted\left( {I_k,ascent order by\;{{\bf{x}}_{jk}}} \right)\;do \cr
& \;\;\;\;\;\;\;\;{G_R} \leftarrow {G_R} + {g_j},{H_R} \leftarrow {H_R} + {h_j} \cr
& \;\;\;\;\;\;\;\;{G_L} \leftarrow G - {G_R},{H_L} \leftarrow H - {H_R} \cr
& \;\;\;\;\;\;\;\;score \leftarrow \max \left( {score,{{G_L^2} \over {{H_L} + \lambda }} + {{G_R^2} \over {{H_R} + \lambda }} - {{{G^2}} \over {H + \lambda }}} \right) \cr
& \;\;\;\;end \cr
& end \cr
& Output:\; split\_value\; and\; default \;directions\; with\; max \; score} $$
论文后续内容为系统部分(包括并行化、cache-aware加速、数据块预处理,需要结合代码研读)、实验(在不同的数据集上进行了实验,包括分类、LTR、CTR预估)详见论文[11]
代码阅读:
代码易用,注释较完备,支持多种语言,目前仍在持续集成和更新,其中稀疏矩阵存储为CSR格式(见附录思考[2])。
很多核心的机器学习函数复用了作者的另一个机器学习库DMLC(Distributed Machine Learning Common Codebase),和参考[12]中介绍代码版本对比,运用较多通用的工厂类方法(见附录思考[3]),草草介绍下主体代码组成,下一篇会进行详细拆解:
附录
引文
[1] Panda, Biswanath, et al. “PLANET: massively parallel learning of tree ensembles with MapReduce.” Proceedings of the Vldb Endowment 2.2(2009):1426-1437.
[2] Tyree, Stephen, et al. “Parallel boosted regression trees for web search ranking.” International Conference on World Wide Web ACM, 2011:387-396.
[3] Ye, Jerry, et al. “Stochastic gradient boosted distributed decision trees.” ACM Conference on Information and Knowledge Management, CIKM 2009, Hong Kong, China, November 2009:2061-2064.
[4] Johnson, Rie, and Z. Tong. “Learning Nonlinear Functions Using Regularized Greedy Forest.” IEEE Transactions on Pattern Analysis & Machine Intelligence 36.5(2013):942-54.
[5] Friedman, Jerome H., and B. E. Popescu. “Importance Sampled Learning Ensembles.” (2003).
[6] Li, Ping, C. J. C. Burges, and Q. Wu. “McRank: Learning to Rank Using Multiple Classification and Gradient Boosting.” Advances in Neural Information Processing Systems (2007):897-904.
[7] Bekkerman, Ron, M. Bilenko, and J. Langford. “Scaling up machine learning: parallel and distributed approaches.” ACM SIGKDD International Conference Tutorials ACM, 2011:1-1.
[8] Tyree, Stephen, et al. “Parallel boosted regression trees for web search ranking.” International Conference on World Wide Web ACM, 2011:387-396.
[9] Greenwald, Michael. “Space-efficient online computation of quantile summaries.” Acm Sigmod Record 30.2(2001):58–66.
[10] Zhang, Qi, and W. Wang. “A Fast Algorithm for Approximate Quantiles in High Speed Data Streams.” (2007):29-29.
[11]Chen, Tianqi, and C. Guestrin. “XGBoost: A Scalable Tree Boosting System.” (2016).
[12] xgboost导读和实战(百度云地址),王超,陈帅华
[13] xgboost代码参数说明, @zc02051126译
[14]xgboost: 速度快效果好的boosting模型,何通
[15]Introduction to Boosted Trees, 官网
思考
[1].不能直接看明白,手痒推导一把就通顺多了。函数$f(x)$在$x_0$处的二阶展开式为:$$f\left( x \right) = f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f''\left( {{x_0}} \right){\left( {x - {x_0}} \right)^2}$$
我们对$l(y_i, x)$在${\hat y}^{(t-1)}_i$处进行二阶展开得到
$$l({y_i},x) = l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right) + {{\partial l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right)} \over {\partial {{\hat y}^{\left( {t - 1} \right)}}}}\left( {x - {{\hat y}^{\left( {t - 1} \right)}}} \right) + {{{\partial ^2}l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right)} \over {\partial {{\hat y}^{\left( {t - 1} \right)}}}}{\left( {x - {{\hat y}^{\left( {t - 1} \right)}}} \right)^2}$$
令$x={\hat y}^{(t-1)}+f_t({\bf x}_i)$,且记一阶导为${g_i} = {{\partial l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right)} \over {\partial {{\hat y}^{\left( {t - 1} \right)}}}}$,二阶导为${h_i} = {{{\partial ^2}l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right)} \over {\partial {{\hat y}^{\left( {t - 1} \right)}}}}$。
我们得到$l(y_i, {\hat y}^{(t-1)}+f_t({\bf x}_i))$的二阶泰勒展开:
$$l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right) + {g_i}{f_t}\left( {{{\bf{x}}_i}} \right) + {1 \over 2}{h_i}f_t^2\left( {{{\bf{x}}_i}} \right)$$
带入目标函数可得:
$${L^{\left( t \right)}} \simeq \sum\limits_{i = 1}^n {\left[ {l\left( {{y_i},{{\hat y}^{\left( {t - 1} \right)}}} \right) + {g_i}{f_t}\left( {{{\bf{x}}_i}} \right) + {1 \over 2}{h_i}f_t^2\left( {{{\bf{x}}_i}} \right)} \right]} + \Omega \left( {{f_t}} \right)$$
[2]:csr格式是什么?类似的格式有什么,它们之间的区别是什么?
参见:稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB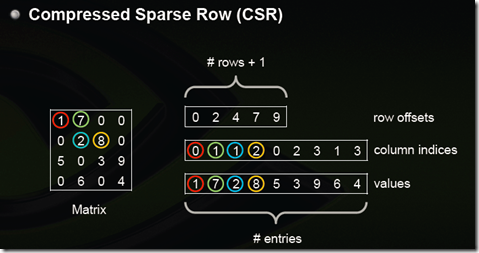
CSR有行偏移,列下标,值三种元素。行偏移数组大小为(总行数目+1),行偏移表示某一行的第一个元素在values里面的起始偏移位置。数值和列号与COO一致,表示一个元素以及其列号。如上图中,第一行元素1是0偏移,第二行元素2是2偏移,第三行元素5是4偏移,第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数,本例中是9。
[3]思考:通用的工厂类,@tenfyzhong
ShawnXiao@baidu